Численное решение прямой задачи рассеяния для больших многосолитонных волновых пакетов на примере нелинейного уравнения Шредингера

Предложен новый подход к численному решению прямой задачи рассеяния для больших многосолитонных волновых пакетов на примере нелинейного уравнения Шредингера. На основе разложения Магнуса построена общая схема произвольного порядка точности для численного решения системы Захарова–Шабата. Для этого в разложении Магнуса удерживается необходимое число слагаемых, также как и в разложении Тейлора волнового поля внутри шага дискретизации, что приводит к возможности получать схемы необходимого порядка.

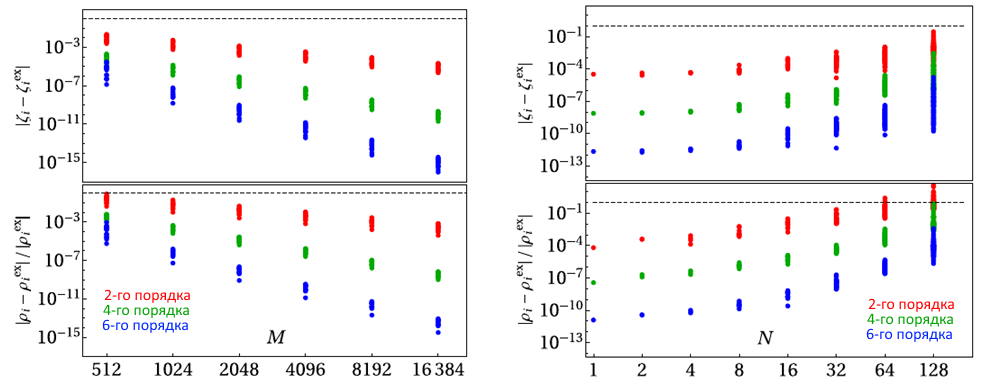
Влияние порядка схемы на численные ошибки определения собственных значений ζi и фаз ρi (а): расчеты проведены для различного количества точек дискретизации M, индекс «ex» обозначает точное значение, расчет проведен для волнового поля (в).	Влияние порядка схемы на численные ошибки определения ζi и ρi  в зависимости от количе-ства солитонов N в волновом поле (б).
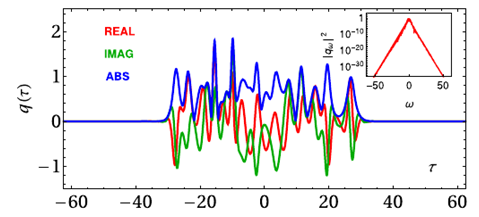	Пример волнового поля q, составленного из 16 солитонов (в).

Представлены численные схемы 4-го и 6-го порядков, что позволяет  находить данные рассеяния больших волновых полей. Построены численные примеры для многосолитонных волновых пакетов вплоть до 128 солитонов. Впервые аккуратно определены не только собственные значения солитонов, но и их фазы, которые необходимы для предсказания эволюции рассматриваемого волнового пакета. Новизна данной работы заключается в создании эффективного алгоритма способного определить параметры солитонов в большом волновом пакете. Показаны успешные примеры для полей, включающих до 128 солитонов. Прежде в литературе были получены результаты для полей с менее чем 10 солитонами. Данный метод позволяет эффективно исследовать результаты численных и экспериментальных работ по исследованию статистики мульти-солитонных полей в различных областях физики. Самыми яркими из них являются исследования волнового поля в задаче о волнах на воде, а также о распространении импульса света в оптоволокне.

ИТ СО РАН, д. ф.-м. н. Мулляджанов Р.И., Гелаш А.А., тел.: 8(383)330-81-28.