Новое полуаналитическое решение задачи о росте пузырька в перегретой жидкости
Представлена математическая модель роста парового пузырька в перегретой жидкости, учитывающая как динамические, так и тепловые эффекты и включающая в себя известные классические уравнения, записываемые с учетом процесса испарения жидкости. Найдено приближенное полуаналитическое решение задачи, построение которого основано на существовании квазистационарного состояния для процесса роста пузырька.
Сформулирована математическая модель роста парового пузырька в изначально однородно перегретой жидкости, одновременно учитывающая как динамические, так и тепловые эффекты и включающая в себя известные классические уравнения – уравнение Рэлея и уравнение энергии, записываемые применительно к рассматриваемой задаче с учетом специфики, связанной с процессом испарения жидкости.
 |
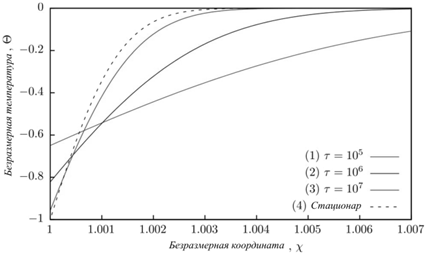 |
| Зависимость радиуса пузырька и плотности пара в пузырьке от времени: сплошная линия – найденное полуаналитическое решение; штриховая линия – решение, полученное в рамках энергетической тепловой модели; штрих-пунктирная линия – решение, полученное в рамках динамической инерционной модели. | Зависимость температуры жидкости от радиальной координаты в различные моменты времени: штриховая линия соответствует стационарному состоянию. |
Показано, что представленная задача сводится к решению системы из трех обыкновенных дифференциальных уравнений первого порядка, что значительно упрощает анализ рассматриваемого процесса. Показано, что полученное решение хорошо согласуется с прямыми численными расчетами в широком диапазоне перегревов и на всех стадиях процесса, включая переходную, учет которой крайне необходим, особенно если рассматривать рост пузырька в сильно перегретой жидкости. Проиллюстрирована динамика изменения температурного поля в объеме жидкости, давления и плотности газа в пузырьке. Найдена зависимость радиуса пузырька от времени.
Показано, что на больших временах процесс роста пузырька определяется исключительно подводом тепла к межфазной границе. Температурное поле вокруг пузырька (в предложенных переменных) становится стационарным, а решение тепловой задачи – автомодельным. Зависимость радиуса пузырька от времени принимает корневой вид, а коэффициент пропорциональности зависит только от числа Якоба, что в предельных случаях соответствует известным решениям других авторов. Однако, при определенных режимных параметрах процесса (в особенности, при больших значениях числа Якоба) данная стадия оказывается недостижимой на обозримых временах.
ИТ СО РАН, д.ф.-м.н., проф РАН Чернов А.А., г.н.с., д.т.н., проф. Лежнин С.И., м.н.с., к.ф.-м.н. Пильник А.А., лаб. Владыко И.В., тел.: +7(383) 330-60-40.